How to calculate the vorticity of a 2D field

How to calculate the vorticity of a 2D field#

Step 1: Create FELiCSMesh, FELiCSSpace and Field

We consider the domain \(\Omega = (0,1) \times (0,1)\), and discretize with triangular elements. The 2D velocity field is a \(P2\) finite element vector field and the magnitude of the vorticity has been stored in a \(P2\) finite element scalar field.

from FELiCS.SpaceDisc.FELiCSMesh import FELiCSMesh
from FELiCS.SpaceDisc.FEMSpaces  import createFunctionSpace
from FELiCS.Fields.Field         import Field
from FELiCS.IO.Reader            import Reader

meshFileName = "./square_mesh.msh"
coordinateSystemName = "Cartesian"

# Create a FELiCS mesh from the gmsh file
mesh = FELiCSMesh(coordinateSystemName, meshFileName)

scalarSpace = createFunctionSpace(mesh, degree=2, dim=1)
vectorSpace = createFunctionSpace(mesh, degree=2, dim=2)

phiVec = Field(vectorSpace, mesh=mesh, name="function_2d")
phiVec.importData(Reader(), "input")


Info     | FELiCSMesh.py          | __init__                   (line 94  ) : Opening mesh file: ./square_mesh.msh
Info     | FELiCSMesh.py          | __init__                   (line 102 ) : Mesh contains 513 nodes and 1024 elements





(<FELiCS.Fields.Field.Field at 0x7ca0d41542d0>, [])

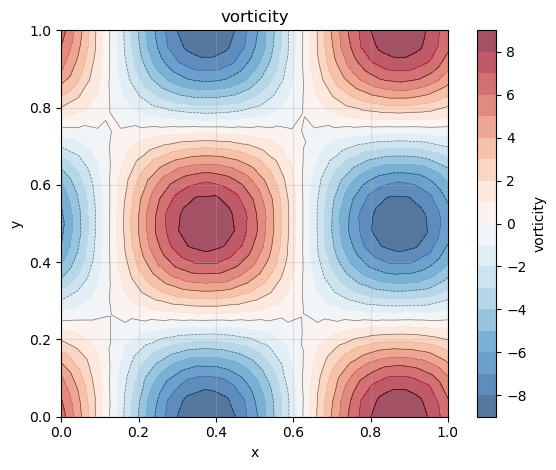
Step 2: Computing the vorticity and comparison with the analytical results.

For a 2D velocity field given by \(\vec{\textbf{u}} = (u, v)\), the vorticity \(\omega\) is defined as

\[ \omega = \nabla \times \vec{\textbf{u}} = (\frac{\partial u}{\partial y} - \frac{\partial v}{\partial x}) \hat{z}, \]

where \(\hat{x}, \hat{y}, \hat{z}\), represent the unit vectors along the Cartesian coordinate axes in 3D space. However, for a 3D velocity field given by \(\vec{\textbf{u}} = (u, v, w)\), the vorticity \(\omega\) is defined as

\[ \omega = \nabla \times \vec{\textbf{u}} = \left( \frac{\partial w}{\partial y} - \frac{\partial v}{\partial z} \right) \hat{x} + \left( \frac{\partial u}{\partial z} - \frac{\partial w}{\partial x} \right) \hat{y} + \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \hat{z} \]
vorticity = phiVec.getVorticityField()

Step3. Postprocessing via plotting contour plots

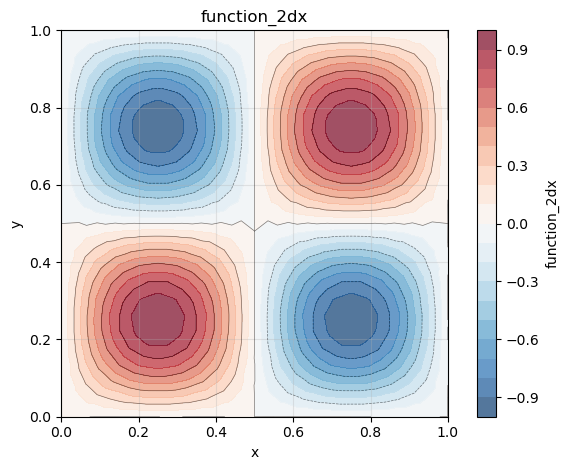
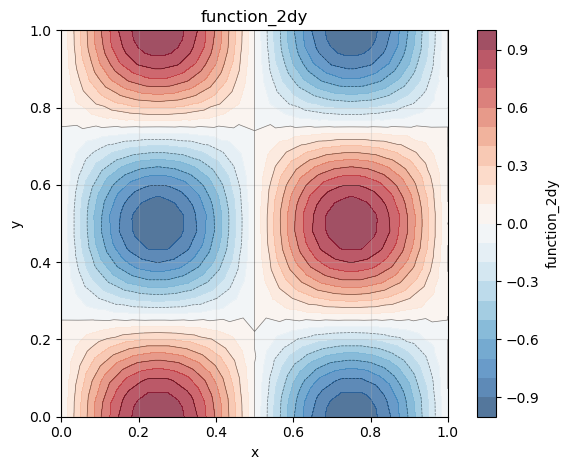
We plot two 2D color plots of the velocity and vorticity magnitudes respectively.

[phi_x, phi_y] = phiVec.getListOfSubFields()

phi_x.plot()
phi_y.plot()
vorticity.plot()

png

png

png